Quizá te hayas preguntado alguna vez cómo es posible que tengamos imágenes muy detalladas (y de muy alta resolución) de galaxias muy distantes gracias al telescopio Hubble y, sin embargo, es incapaz de hacer imágenes igual de buenas de los planetas del Sistema Solar, que están mucho más cerca. ¿Cómo es posible?
Cuando el tamaño (y la distancia) sí importan
Aunque hay que tener en cuenta diversos factores, el más importante para explicar por qué es posible que el telescopio Hubble pueda hacer esas fotos tan espectaculares de galaxias, pero no pueda mostrar los planetas con tanto detalle, es el tamaño y la distancia de los objetos de los que estemos hablando. Hasta hace poco, se solía hablar especialmente de Plutón porque, hasta la llegada de la sonda New Horizons el año pasado, no teníamos imágenes en alta definición, pero ya no es el caso.
Así que en este artículo hablaré de Neptuno, en comparación con la galaxia de Andrómeda, para poder ilustrarlo con ejemplos que sigan siendo válidos en la actualidad (pero lo cierto es que con casi cualquier otro objeto del Sistema Solar y cualquier galaxia de la que tengamos una buena imagen, vamos a poder hacer el mismo cálculo y llegar a las mismas conclusiones). Básicamente, podemos reducirlo a dos factores: la distancia y tamaño del objeto del que estemos hablando, y la capacidad de resolución de imagen de la cámara que lo esté fotografiando.
Con la distancia y el tamaño del objeto podemos saber cuánto espacio ocupa en el cielo, pero la mejor forma de explicarlo es recurriendo a un ejemplo práctico con Neptuno (el planeta más distante del Sistema Solar) y la galaxia de Andrómeda (la galaxia más cercana a la Vía Láctea), así que vamos a ellos.
Los objetos vistos por el telescopio Hubble

Neptuno, en color natural, con tres de sus satélites, visto por el telescopio Hubble.
Crédito: NASA, ESA, E. Karkoschka (University of Arizona), y H.B. Hammel (Space Science Institute, Boulder, Colorado)
Esta imagen de Neptuno (en la que también aparecen varios de sus satélites) fue tomada por el telescopio Hubble entre el 29 y el 30 de abril de 2005. No he podido consultar la distancia exacta a la que se encontraba Neptuno en esa fecha (porque el simulador del Sistema Solar de la NASA no parecía funcionar en el momento de escribir este artículo), pero sabemos que la distancia media entre la Tierra y Neptuno es de 4.400 millones de kilómetros. También sabemos que el planeta tiene un diámetro de 49.244 kilómetros, así que el tamaño que ocupa en el cielo lo podemos expresar como un ratio entre ambos factores. Es decir, dividimos su tamaño por la distancia a la que está.
El resultado que nos arroja la operación (49244 km / 4400 millones de km) es 0,00001119. Ahora, comparémoslo con la galaxia de Andrómeda de la que, en 2015, el telescopio Hubble tomó la imagen que puedes ver aquí debajo:

Porción de la galaxia de Andrómeda fotografiada por el telescopio Hubble. Crédito: NASA, ESA, J. Dalcanton, B.F. Williams, y L.C. Johnson (University of Washington), el equipo PHAT, y R. Gendler
Si la quieres ver en todo su esplendor (es una imagen de muy alta resolución), puedes acceder a ella en este enlace (tiene casi 200 megas de tamaño). La galaxia de Andrómeda tiene un tamaño de 220.000 años-luz y está a una distancia de 2,5 millones de años-luz. En este caso en particular, la imagen que he enlazado cubre un area de 48.000 años-luz, y es lo que usaremos para el cálculo, que nos arroja una cifra (48000 años-luz / 2,5 millones de años-luz) de 0,0192. O lo que es lo mismo, esta porción de la galaxia de Andrómeda ocupa, en el cielo, un tamaño 1715 veces más grande que Neptuno.
La mejor imagen que tenemos del planeta más distante del Sistema Solar no es ésa, si no la que acompaña este párrafo, que fue tomada por la sonda Voyager 2. En el momento de tomar esta imagen (el 30 de octubre de 1998), la sonda se encontraba a 4,4 millones de kilómetros. Pero, ¿cómo de bien ve el telescopio Hubble? Aquí es donde entra en juego el segundo factor del que hablaba al principio, la capacidad de resolución del instrumento.
La imagen de la galaxia de Andrómeda está tomada con la Advanced Camera for Surveys, que tiene una resolución de 0,05 segundos de arco. Un segundo de arco es 1/3600 de un grado. Es decir, un único pixel de esa imagen muestra 0,05 segundos de arco. Lo siguiente que podemos hacer es convertir esta cifra en radianes para poder ver el tamaño que ocupa cada cosa en una imagen. El cálculo, por si te interesa, es 0,05*(1/3600)*(2pi/360), que nos da 0,24 microradianes.
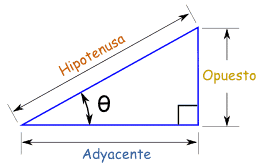
¿Por qué hacemos esta conversión? Es un truco que podemos hacer con las medidas angulares cuando hablamos de ángulos muy pequeños. Cuando el ángulo es muy pequeño, la tangente del ángulo es aproximadamente la misma que el ángulo (cuando lo estamos expresando en radianes). La tangente de un ángulo es la longitud del lado de un triángulo rectángulo opuesto al ángulo, dividido por la longitud del lado adyacente al ángulo, o dicho con una imagen, es ésto:
En el caso de la galaxia de Andrómeda, el ratio que hemos calculado antes entre el tamaño de la región fotografíada y su distancia de nosotros, 0,0192, nos dice el ángulo en el que la galaxia subtiende en el cielo, expresado en radianes. Si lo dividimos por la resolución angular en radianes por píxel de la cámara, 0,00000024, obtenemos 80.000 píxeles. Sin embargo, para Neptuno (que también fue fotografiado con la misma cámara), haciendo ese mismo cálculo obtenemos poco más de 46 píxeles (46,625 exactamente).
Así que ésta es la explicación por la que podemos tener imágenes detalladísimas de lugares que están a millones de años-luz de distancia y, sin embargo, necesitamos mandar una sonda a los planetas y satélites del Sistema Solar para poder verlos en todo su detalle. Las galaxias están muy lejos, sí, pero también son, comparativamente, muchísimo más grandes que los mundos que nos rodean.
Referencia: The Planetary Society








El problema de los telescopios es la atmósfera terrestre
Leído.
¿Y sale más barato construir y mandar una sonda (con el tiempo que conlleva llegar hasta allí) que construir un telescopio con una resolución más acorde a los objetos más cercanos?
Puedes explicarlos en palabras para el común de la gente o con u ejemplo o analogía. Gracias.