Si lo pudiésemos ver en su escala más grande, esa en la que las galaxias no son más que meros puntos de luz, seríamos capaces de ver la forma que tiene el universo. Como no tenemos esa posibilidad, la cosmología se plantea esa pregunta por nosotros, y tenemos alguna que otra idea…
El universo es plano

Esta imagen del telescopio Hubble acumula 555 horas de exposición de una región del cielo aparentemente vacía. Todos los objetos son galaxias, con la excepción de dos estrellas (indicadas por su forma puntiaguda).
El espacio fotografiado es, aproximadamente, el que ocupa un palillo a la distancia de tu brazo extendido.
Crédito: NASA
No, no pienses que he rematado el artículo en el primer título, porque no es una afirmación tan simple. Hasta donde sabemos (gracias a los datos del satélite Planck, que estuvo en órbita desde el año 2009 hasta 2013), el universo observable es completamente plano. Sin embargo, la luz que ha llegado hasta nosotros puede ser simplemente una pequeña parte del conjunto del universo, y eso nos obliga a hacer lecturas mucho más complejas.
A fin de cuentas, ¿qué quiere decir que un objeto de tres dimensiones sea plano, ¿cómo podemos medir la forma que tiene? En realidad, basta con tener claro qué entendemos por plano. La pantalla en la que estás leyendo este artículo es plana, mientras que la Tierra, como sabes, es curva. Matemáticamente, es posible cuantificar esa curvatura (o falta de) y es un ejercicio muy útil para poder analizar la forma del universo.
Líneas paralelas
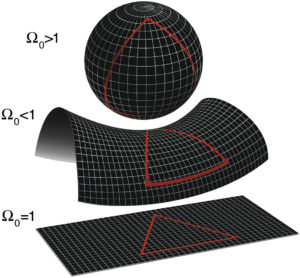
La forma del universo depende de su densidad. Si es superior a la densidad crítica, está cerrado y se curva como una esfera. Si es inferior, como un sillín, pero si la densidad es igual a la crítica, entonces es completamente plano y se extiende infinitamente en todas las direcciones.
Crédito: NASA/WMAP Science Team
Si coges una hoja de papel y dibujas dos líneas paralelas, y las dejas avanzar, estarán siempre perfectamente separadas, al menos hasta que te quedes sin papel sobre el que seguir dibujándolas. Esa es la definición de una línea paralela, podemos extenderla hasta el infinito y en ningún momento se acercará a la otra línea. Pero, si repetimos ese mismo ejercicio en la superficie de la Tierra, comenzando en algún lugar del ecuador, y dibujamos dos líneas paralelas que vayan hacia el polo norte, el resultado es diferente.
A medida que esas líneas continúan, a pesar de ser completamente rectas y nunca girar hacia ningún lado, terminarán cruzándose en el Polo Norte. Esa intersección está provocada por la propia curvatura de nuestro planeta, provocando que nuestras líneas paralelas dejasen de serlo. Por tanto, podemos concluir que la Tierra es curva. Lo opuesto es una superficie en forma de sillín (o montura de caballo). En esa superficie sucede lo contrario. Las líneas que comienzan paralelas se terminan separando.
Así que, dicho de otra manera, podemos medir lo plana que es una estructura observando cómo se comportan las líneas paralelas. En nuestro universo en tres dimensiones, podemos hacer ese mismo ejercicio observando haces de luz. Si, por ejemplo, tenemos dos láseres que comienzan en puntos paralelos, su comportamiento nos podría servir para comprender cuál es el aspecto del cosmos.
El estudio de lo más grande
Medir la forma del universo es una de las preguntas a la que se enfrenta la cosmología. Es el estudio del universo en su conjunto. Es decir, cuando observamos el universo en su escala más grande, no tenemos en cuenta ni los sistemas estelares, ni las galaxias, ni los agujeros negros, ni estrellas de neutrones… porque son pequeños baches, casi imperceptibles, que no tienen impacto alguno en este tipo de preguntas.
El universo tiene multitud de deformaciones, en el espacio-tiempo, que lo alejan de ser perfectamente plano. En cualquier lugar en el que haya masa o energía, nos encontramos con la correspondiente curvatura del espacio tiempo (tal y como dice la teoría de la relatividad de Albert Einstein). Así que nuestros láseres chocarían el interior de un agujero negro, o se curvarían en ángulos extraños al encontrarse con un par de galaxias en su recorrido.
Pero si ignoramos esos efectos en una escala tan pequeña (recuerda, estamos hablando del universo en su conjunto, algo tan grande que las galaxias son simples puntos de luz) y observamos todo el conjunto, podemos ver que, al examinar la luz más antigua, como puede ser el caso de la radiación cósmica de fondo de microondas, que ha estado viajando por el universo durante más de 13.800 millones de años, podemos hacernos una buena idea de la forma del universo. La respuesta, hasta donde podemos ver, con un margen de error muy pequeño. es que es plano.
Plano pero… ¿curvado?
Pero hay más. No es lo mismo una esfera que un cilindro. ¿Recuerdas la hoja de papel que hemos utilizado como ejemplo para definir nuestras líneas paralelas?, si la coges y la enrollas para que un extremo toque al otro, tendrás un cilindro. Si te fijas en las líneas que habías dibujado, verás que siguen siendo perfectamente paralelas, porque un cilindro es plano… por extraño que pueda sonar.
Es una distinción importante. Una cosa es la geometría, el comportamiento de esas líneas paralelas, y otra cosa es la topología, la forma en la que podemos torcer y manipular un espacio (como hemos hecho con nuestra hoja de papel en este ejemplo). Hemos medido con mucha precisión la geometría del universo (por eso sabemos que es plano), pero no hemos medido su topología. De hecho, no podemos determinarla por medio de observaciones, y no hay leyes de la física que nos digan cuál podría ser su forma.
Si seguimos con ese papel, podemos conectar sus extremos de varias maneras diferentes. Conectando un extremo, tenemos un cilindro. Si giramos uno de los extremos antes de conectarlo, hemos creado una banda de mobius. Si conectamos las dos dimensiones, es decir, la parte superior e inferior del papel, y la parte izquierda y derecha, lo que hemos creado es un toro (la clásica forma de un donut).
En un universo de tres dimensiones tenemos muchas más opciones que en un papel de dos. En concreto, hay 18 posibilidades. Las bandas de mobius y las botellas de Klein (entre otros) son ejemplos de topologías complejas que tienen algo en común. Si viajas lo suficiente en cualquier dirección, vuelves al lugar en el que te encontrabas. En el caso de dimensiones alteradas, al regresar a tu punto inicial te encuentras boca abajo a pesar de no haber hecho algo así en ningún momento.
Hemos intentado ver si nuestro universo está conectado de esa manera, pero no vemos copias de galaxias, ni vemos que la radiación de fondo de microondas se intersecte a sí misma. Si el universo tiene una de estas formas complejas, es en una escala muchísimo más grande de lo que podemos observar. O lo que es lo mismo, a pesar de que sabemos que es plano, eso no quiere decir que su forma pueda ser muy enrevesada. Algo que, al menos por ahora, no sabemos…
Referencias: LiveScience









Después de buscar mucha información sobre el tema, aquí encontré la explicación más clara. Gracias!
Me mareé un poco leyendo ese artículo. Jajajaja